√100以上 図形 の 角度 の 求め 方 228254-図形の角度の求め方
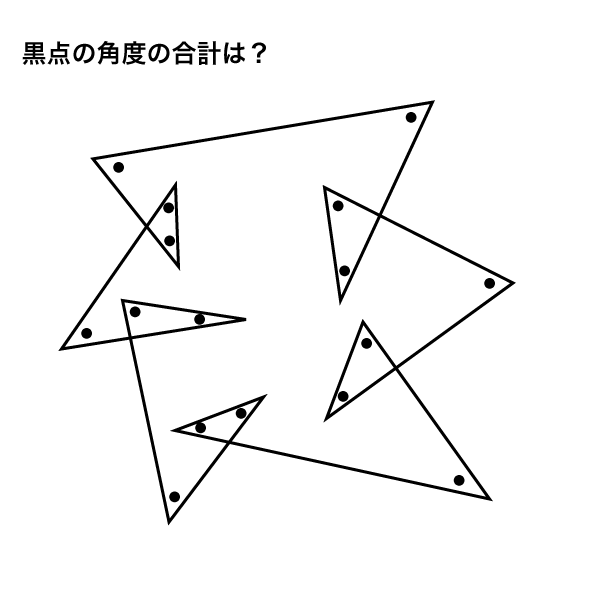
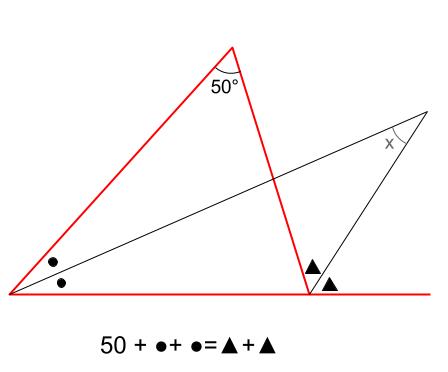
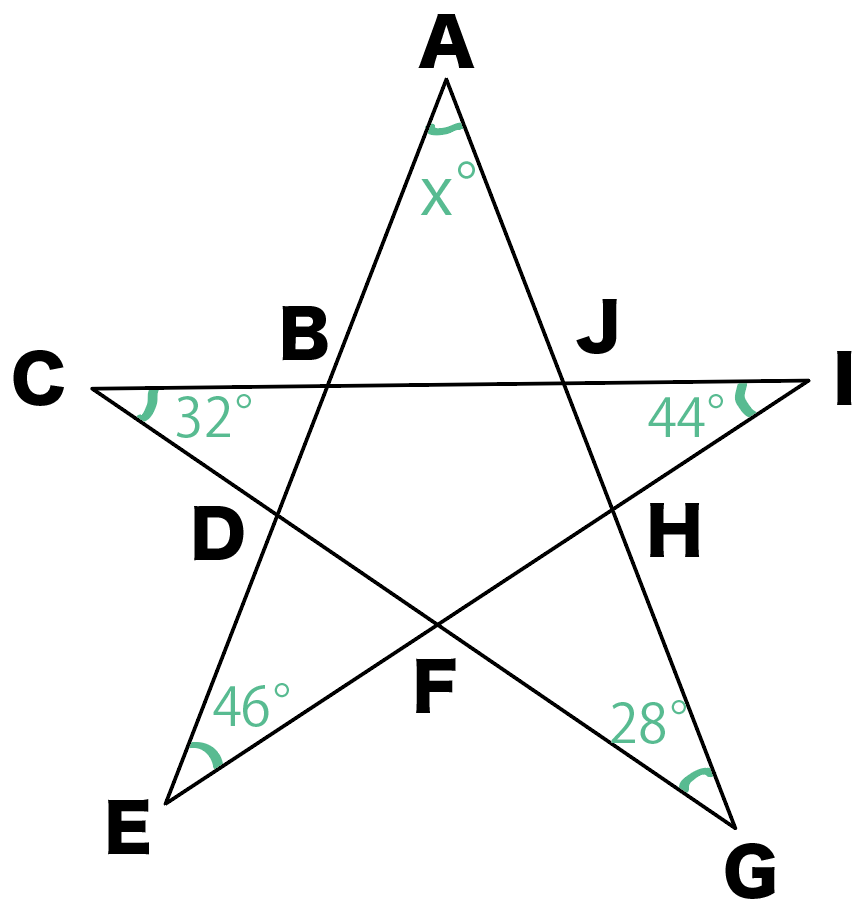
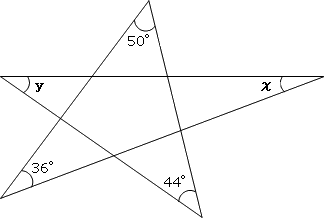
角度情報がない図形の合計の角度 星形多角形 受験算数入門
正多角形はすべての角の大きさが等しいので、これをで割ります。 180× (−2)÷ =9 ×18=162° 180 × ( − 2 ) ÷ = 9 × 18 = 162 ° 答えは 162° 162 ° です。 平面図形の角や面積などの問題は掛け算や割り算が複雑になってくるので、計算の順番などを工夫しましょう。 ちなみに多角形の内角の角度を求める練習問題を用意しました。 問題はランダムで変わる図形の角と面積 三角形や四角形の面積の求め方や、角度のはかり方をおぼえましょう。 動画で学ぼう! (NHK for School) (外部サイト) NHK 1459 三角を四角く マテマティカ2 三角形の面積の求め方を、四角に直すことで原理から考える。
図形の角度の求め方
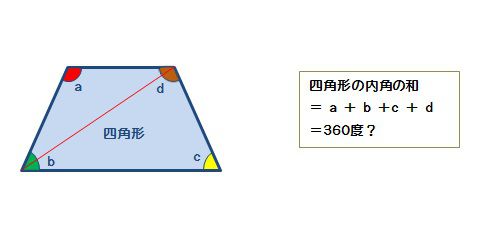
図形の角度の求め方- まず初めに、正五角形の1つの内角の大きさを求めます。 正五角形の内角の和は、 180°× (52)=540° 正五角形なので一つひとつの内角は等しいでの、 540÷5=108° 上の図の四角形ABCDで、①+108×3=360°になるので (四角形の内角の和は180°× (42)=360°だから)、①の角度は、 360°108×3=36° よって、 答え ①=36° まとめ いかがだったでしょうか? どんなに難しい角 dr リード 円の性質円周角の角度の求め方の3つのパターン
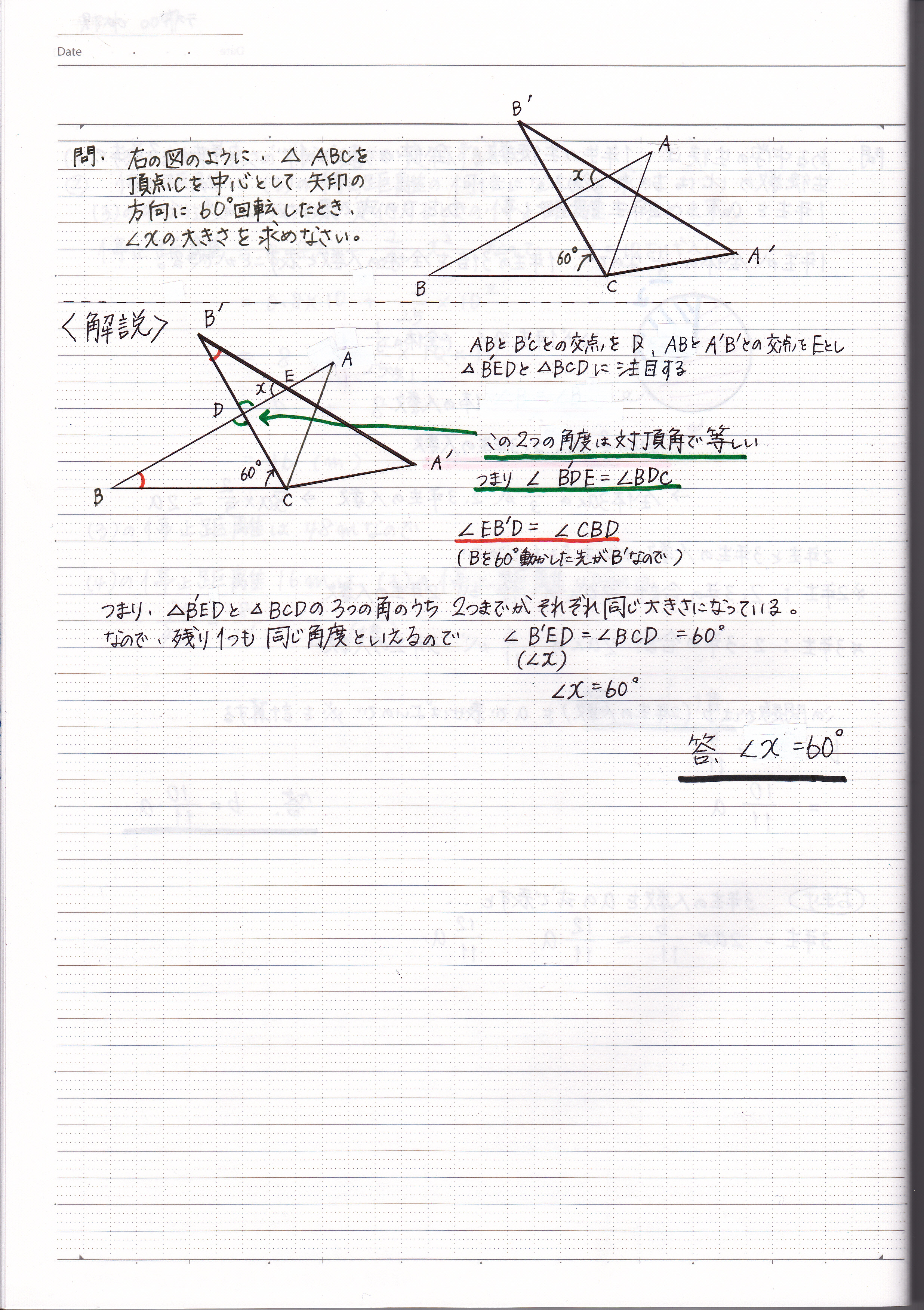
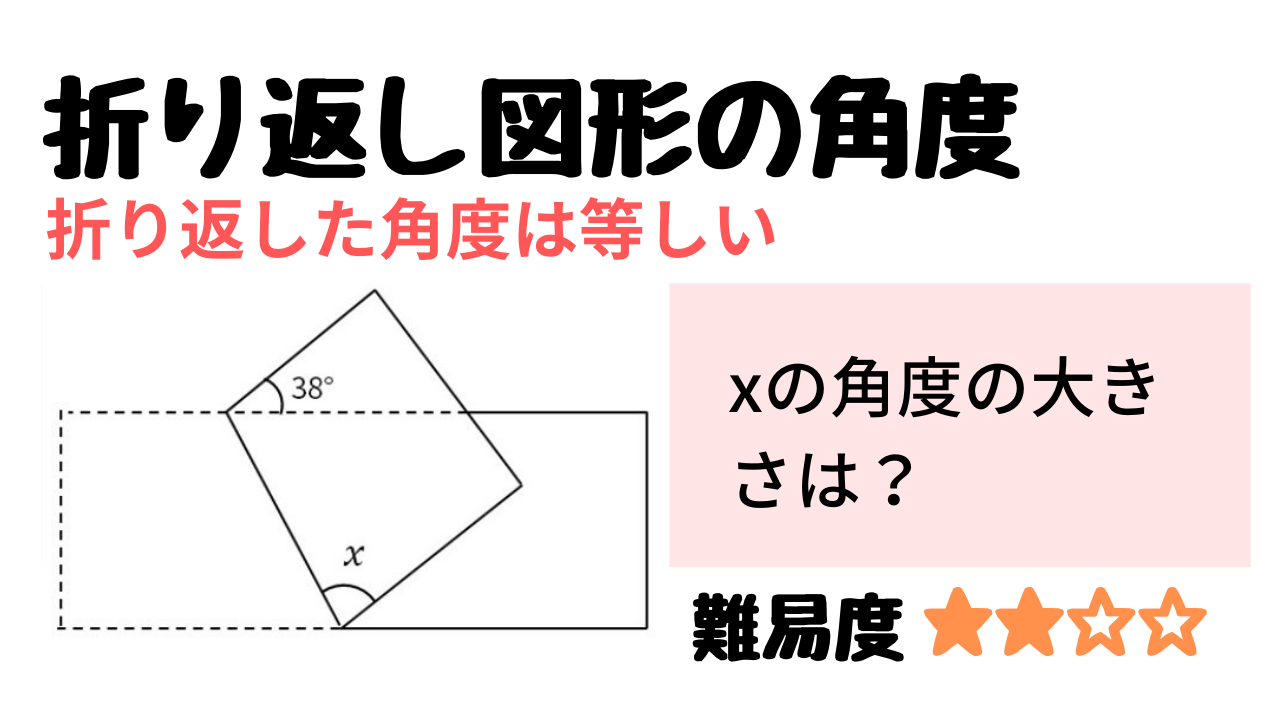
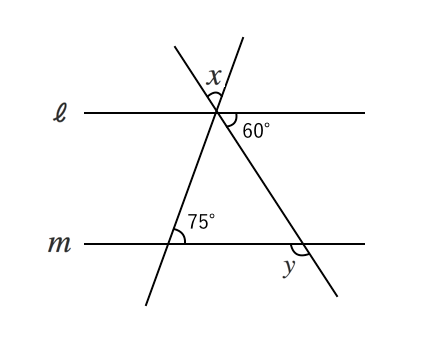
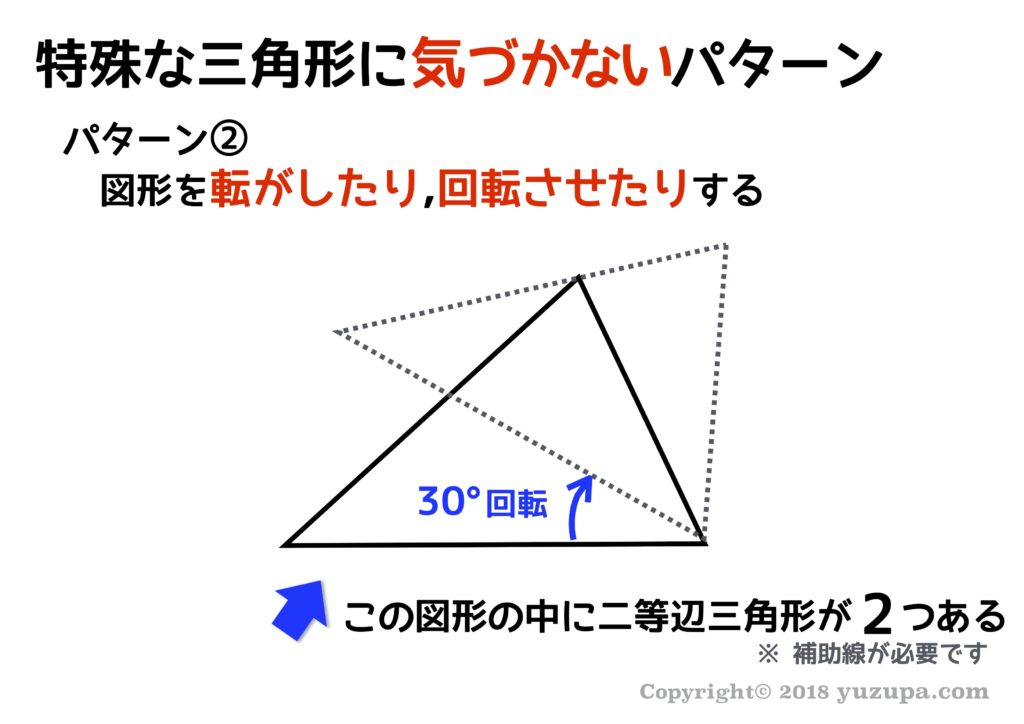
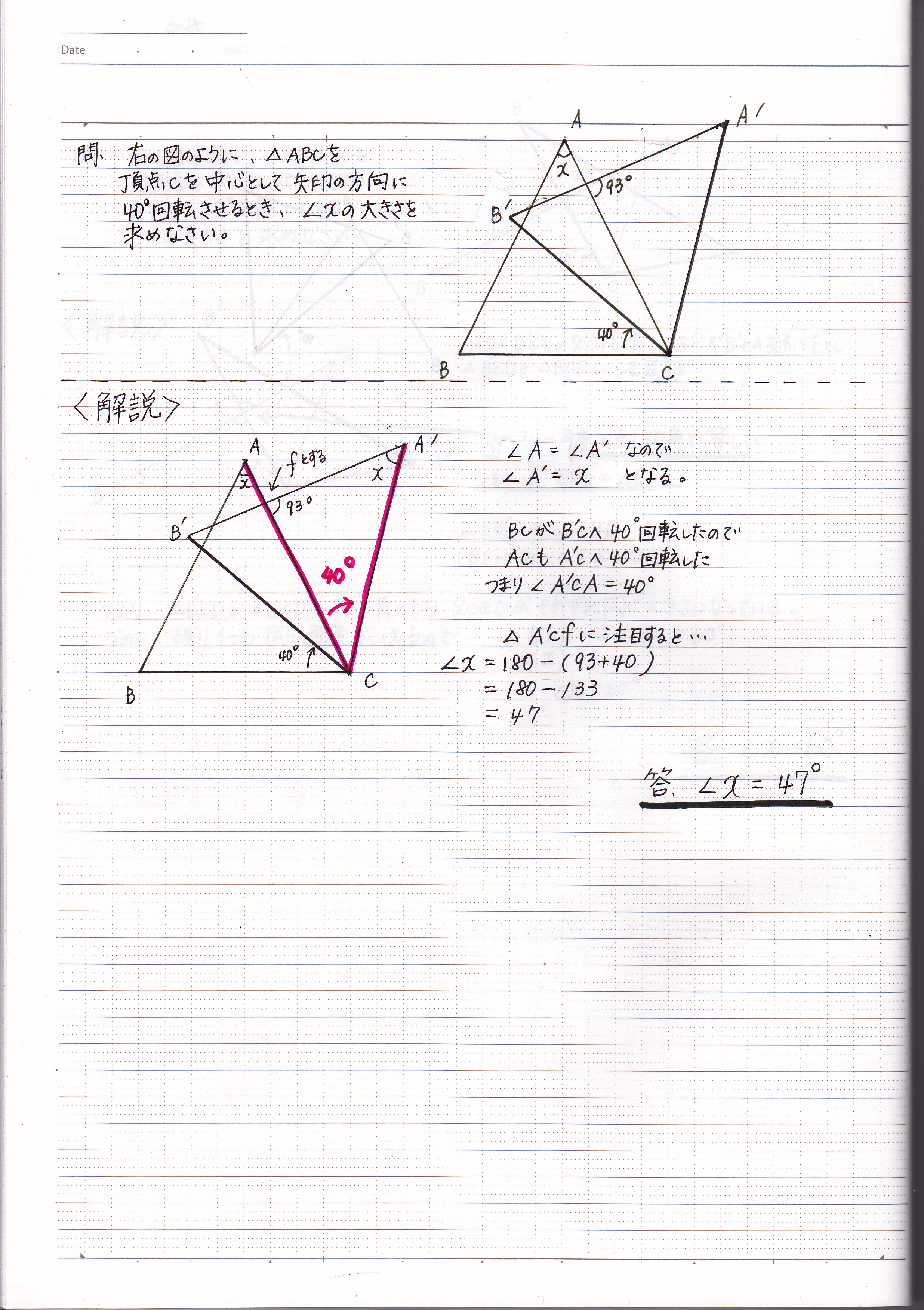
回転する図形の角度の求め方 現役塾講師のわかりやすい中学数学の解き方
直線の角度は180°です。 そのため、∠Aの角度は以下のように計算できます。 180 ° − 1 ° = 60 ° 同じように考えると、∠Bは以下のように計算できます。 180 ° − 1 ° = 60 ° 今回は1°として計算しましたが、別の角度と仮定して計算したとしても、∠Aと∠Bは必ず同じ角度になります。 こうして対頂角は必ず同じ角度になると証明できます。 同位角と錯角の関係を理解する 対頂角を理解したら、次正多角形の内角1つ分の大きさは 外角 このように求めてやることができます。 正三角形の場合 まず、外角1つ分の大きさを求めて 180°から外角1つ分の大きさを引いてやります。 先ほど外角の求め方のところで 1°になるということがわかっているので 正三角形の内角1つ分の大きさは となります。 正五角形の場合 正五角形の1つ分の外角は72°となるので 内角1つ分の大きさは となります。 同様に 正 画像の図形の内角の和は900度なのですが 求め方が分かりません。 答えの式には180(72)=900 となるのですが、なぜ七角形になるのでしょうか? 分かる方ご回答お願いします。
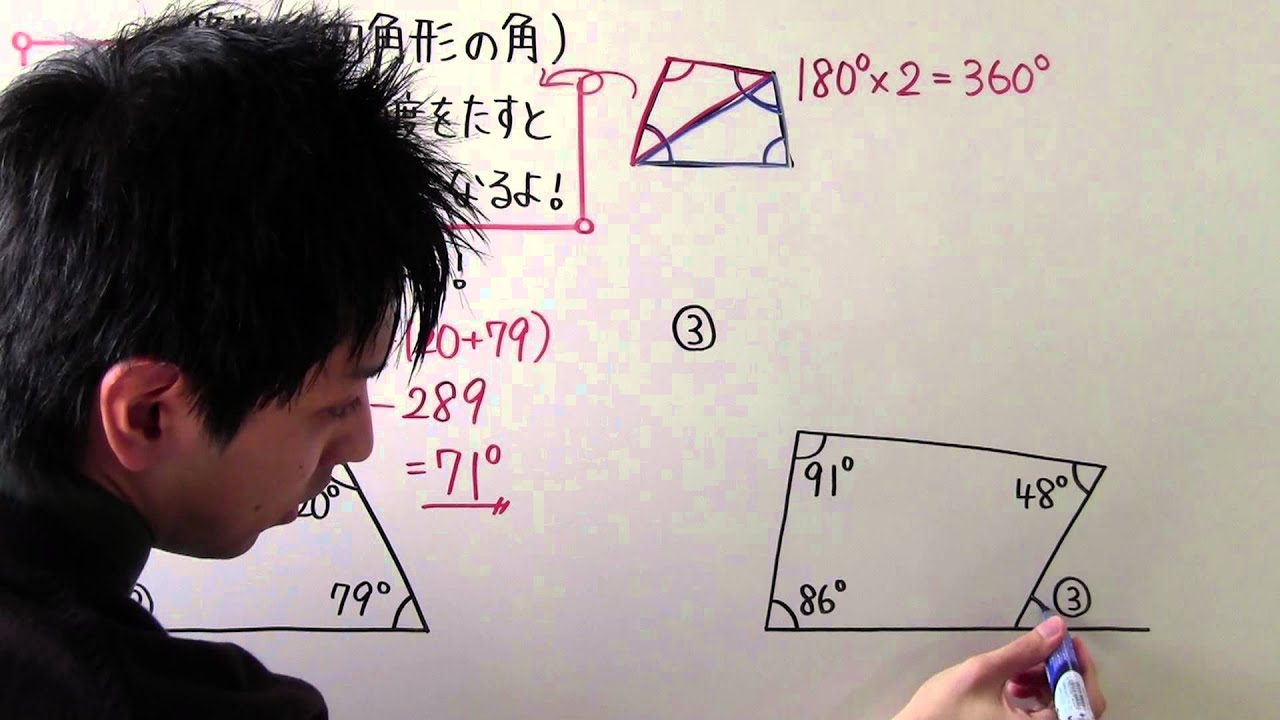
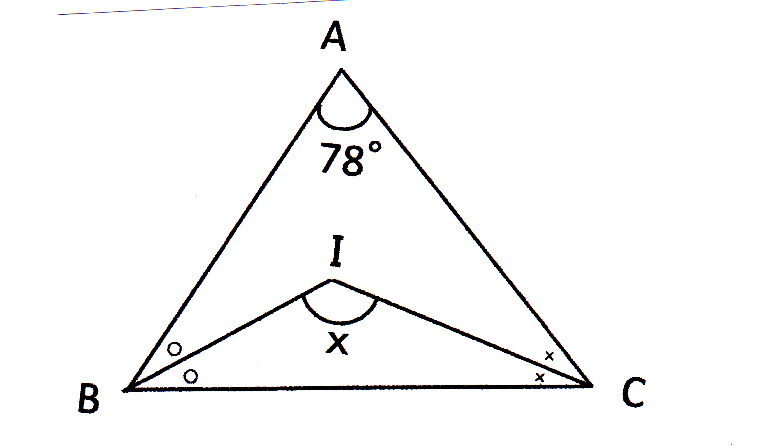
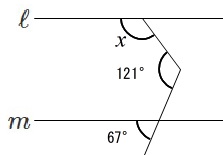
図形の製図 ご意見・ご感想 角度を測定するより、高さと底辺を測定する方が簡単なので、とても役に立ちました。 diy家具設計で、筋交い部の角度と長さを求めました。5年算数「図形の角」「三角形四角形の角」の教え方をアニメでわかりやすく解説しています。保護者の方や学習ボランティアの方の参考になれば幸いです。 2.多角形の内角の和の求め方 教え方1 三角形の3つの角の角度をたすと何度になるか考えさせ問題3 下の図の角xの角度を求めなさい。 → 解答 問題4 下の図の角xの大きさを求めなさい。ただし、同じ印の付いた角の大きさは等しいものとします。解答
図形の角度の求め方のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「図形の角度の求め方」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
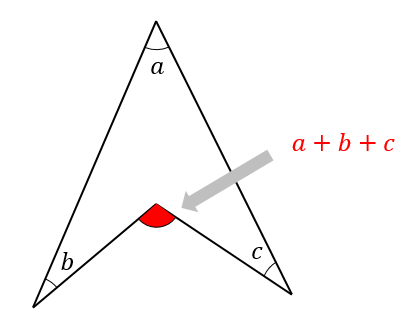
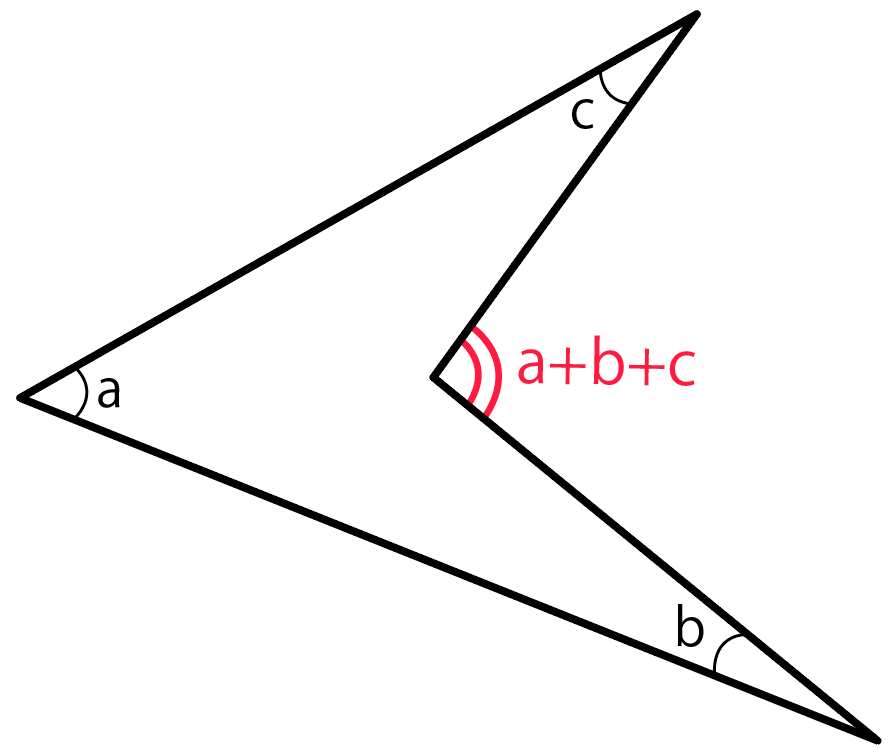
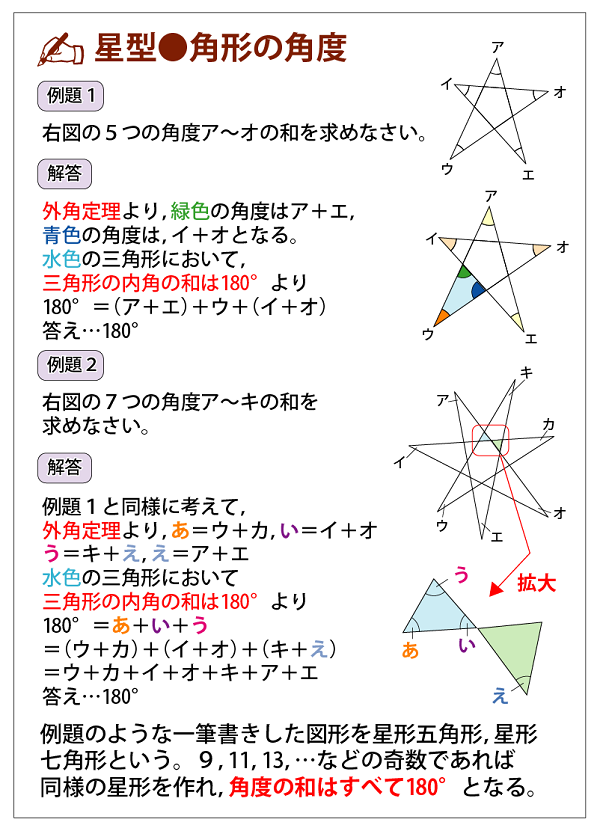
三平方の定理、あなたはちゃんと説明できますか?問題、解けますか? 中学数学の中でも、図形問題はなかなか難しいものの1つです。三平方の定理は、その図形問題を解く際の基礎であり、必要不可欠な知識で 1911 ロン 1つ1つの角は求められませんが、5つの角の和であれば求めることができましたね! 図形の角度の和も求めよう! もう一題やってみましょう! 今度は星形ではない形にしてみました。 これもよく見かける問題ですね。 印のつけてある角の和を求めてみ
Incoming Term: 図形の角度の求め方, 図形の角度の求め方 中学生, 図形の角度の求め方 小学生, 図形の角度の求め方 小学6年,
コメント
コメントを投稿